- Home
- Publications
- PAGES Magazine
- Transient State Estimation In Paleoclimatology Using Data Assimilation
Transient state estimation in paleoclimatology using data assimilation
Stefan Brönnimann, J. Franke, P. Breitenmoser, G. Hakim, H. Goosse, M. Widmann, M. Crucifix, G. Gebbie, J. Annan and G. van der Schrier
PAGES news
21(2)
74-75
2013
Stefan Brönnimann1, J. Franke1, P. Breitenmoser1, G. Hakim2, H. Goosse3, M. Widmann4, M. Crucifix3, G. Gebbie5, J. Annan6 and G. van der Schrier7
Data assimilation methods used for transient atmospheric state estimations in paleoclimatology such as covariance-based approaches, analogue techniques and nudging are briefly introduced. With applications differing widely, a plurality of approaches appears to be the logical way forward.
Reliable estimations of past climate states are the foundations of paleoclimatology. Traditionally, statistical reconstruction techniques have been used, but recent developments bring data assimilation techniques to the doorstep of paleoclimatology. Here we give a short overview of transient atmospheric state estimation in paleoclimatology using data assimilation. An introduction to data assimilation as well as applications for equilibrium state estimation and parameter estimation are given in the companion papers to this special section (see also Wunsch and Heimbach 2013).
 |
|
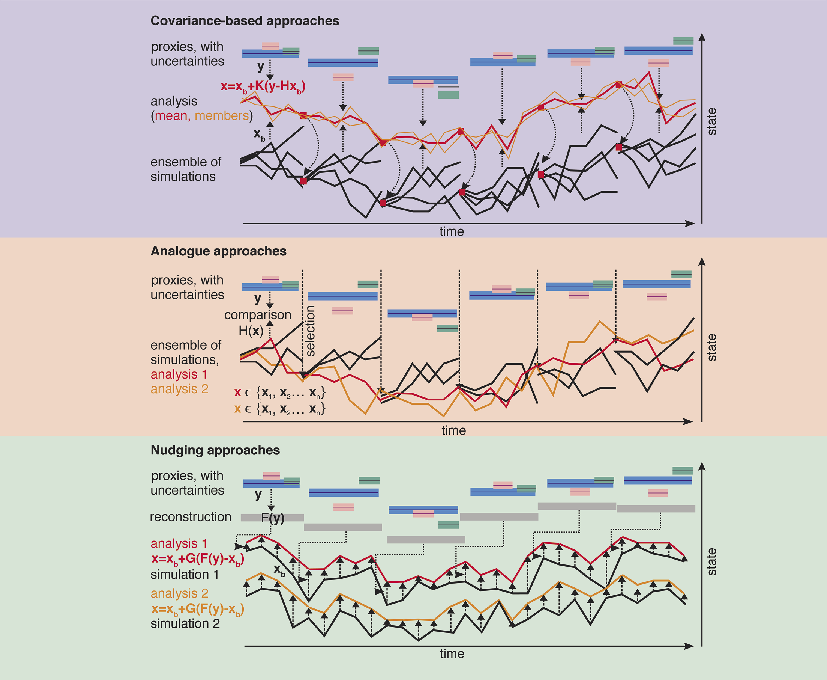
Figure 1: Schematic overview of assimilation approaches. Arrows denote steps in the procedure. |
Data assimilation combines information from observations with numerical models to obtain a physically consistent estimate (termed “analysis”) of the climate state. It has been hugely successful in generating three-dimensional atmospheric data sets of the past few decades. The “Twentieth Century Reanalysis Project” (Compo et al. 2011) extended the approach as far back as 1871, but there is a limit to further extension, because conventional data assimilation relies on the availability of state observations. Paleoclimate proxies do not capture atmospheric states, but time-integrated functions of states, such as averages, in the simplest case. Therefore, for assimilating proxies, other methods are required than those applied in atmospheric sciences. We briefly present below, three groups of assimilation methods for transient atmospheric state estimation in paleoclimatology: “Classical” covariance-based approaches such as the Kalman Filter or variational techniques; approaches based on analogues such as Particle Filters; and nudging techniques. A schematic view of these methods is given in Figure 1. Note that other methods may be used for the ocean (see Gebbie 2012).
Covariance-based approaches
The assimilation problem can be formulated as a cost function J, assuming Gaussian probability distributions:
J(x) = (x-xb)T B-1 (x-xb) + (y-H[x])T R-1 (y-H[x]) (1)
where x is the analysis, xb is a model forecast, y are the observations (or proxies), H is the observation operator that mimics the observation (or proxy) in the model space, B is the background error covariance matrix and R is the observation error covariance matrix (often assumed to be diagonal). The solution to (1) in the classical Kalman form is:
x = xb + BHT(R+HBHT)-1 (y-Hxb) (2)
where H is the Jacobian of H. Variational approaches can be used to approximate the solution. In the Ensemble Kalman Filter (EnKF), B can be estimated from the ensemble, and each member is updated individually. Normally x is a state vector. However, Dirren and Hakim (2005) have successfully extended the concept to time averages.
Data assimilation entails that x serves as an initial condition for the next forecast step. Focusing on the seasonal scale, Bhend et al. (2012) use the EnKF without updating the initial conditions (termed EKF here), which are no longer important on this scale (rather, predictability comes from the boundary conditions, including sea-surface temperatures). This conveniently allows one to use pre-computed simulations. Because x does not serve as new initial condition, it can be small and can be a vector of averaged model states (e.g. all monthly averages of a season for three variables). H can be a simple proxy forward model, i.e. a time-integrated function of elements of x.
Covariance-based approaches are powerful but computationally intensive and can be sensitive to assumptions (e.g. of Gaussian distributions), to the treatment of covariance matrices, or to the behavior of the observation operator.
Analogue approaches
Reverting to cost function (1), we can also look for an existing x, e.g. by choosing among different ensemble members. The cost function (1) reduces to:
J(x) = (y-H[x])T R-1 (y-H[x]) (3)
for x ϵ {x1, x2,...,xn}
New ensemble members are then generated for the next time step by adding small perturbations to x and the final analysis is a continuous simulation. The Particle Filter (PF, Goosse et al. 2010) approach uses a distribution of x to calculate a weighted sum of cost function contributions to (3).
In the Proxy Surrogate Reconstruction approach (PSR, Franke et al. 2011) and the Best Ensemble Member approach (BEM, Breitenmoser et al., in preparation) pre-computed simulations are used with {x1, x2,...,xn} denoting different slices of a long simulation for PSR or in the case of BEM, the same slice in an ensemble of simulations. The “analysis” in both cases is a sequence of short, discontinuous simulations. In contrast to EnKF, H may be non-differentiable (e.g. H can be a complex forward model driven by the full simulation output). R may be non-diagonal, and x may be very large (e.g. six-hourly model output over a 6 month period). However, to reconstruct the state of systems including a large number of degrees of freedom, these approaches require a huge pool of possible analogues (Annan and Hargreaves 2012).
Nudging approaches
Nudging approaches (Widmann et al. 2010) do not explicitly minimize a cost function. The distance between model state and observations is reduced by adding tendencies to (a subspace of) the model state at each time step, similar to an additional source term in the tendency equations. Following our notation:
x = xb + G (F[y] - x) (4)
where F[y] represents the target field (derived using up-scaling method F from observations or proxies y) in the dimension of the model (sub-)space. G is a relaxation parameter.
The Forcing Singular Vectors method (van der Schrier and Barkmeijer 2005) manipulates the tendency equations as well, but adds a perturbation, which modifies the model atmosphere in the direction of the target pattern only.
Examples
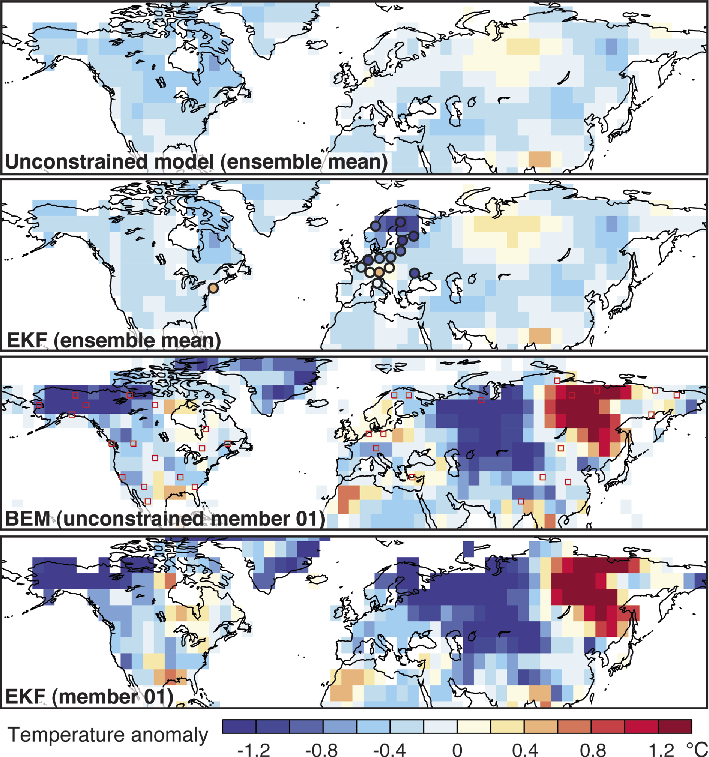
Figure 2 shows April-to-September averages of surface air temperature obtained from two assimilations approaches (EKF and BEM) for the year 1810 relative to the 1801-1830 mean. Both approaches are based on the same ensemble of simulations described in Bhend et al. (2012). The ensemble consists of 30 simulations performed with ECHAM5.4 at a resolution of T63/L31 (ca. 2° x 2°), with sea-surface temperatures and external forcings as boundary conditions.
The unconstrained ensemble mean (Fig. 2 top) shows the effect of boundary conditions, here resulting in cooler than average summer temperatures following the large, but not yet localized volcanic eruption in 1809. Anomalies are small and smooth which is typical for an ensemble mean. The EKF analysis was constrained by historical instrumental observations using Eq. (2). The EKF ensemble mean suggests a more pronounced cooling over northern Europe, but over most regions (due to lack of observations) it is close to the unconstrained ensemble mean. BEM was constrained with tree rings from 35 locations. The VS-lite tree growth model (Tolwinski-Ward et al. 2011) was used as H and Eq. (3) was minimized. BEM identifies member 01 as the best fitting one. This member exhibits large anomalies in Alaska and Eurasia, but due to the small ensemble size little regional skill is expected (Annan and Hargreaves 2012). For instance, it does not fit well with instrumental observations over Europe. The same member in the EKF analysis (Fig. 2, bottom) shows a better correspondence, but we loose the advantage of having the full 6-hourly model output available.
Limitations and future directions
Paleoclimatological applications are much more disparate than atmospheric sciences in terms of time, time scales, systems analyzed, and proxies used. Therefore, a plurality of data assimilation approaches is a logical way forward. However, all approaches still suffer from problems and uncertainties. Ensemble approaches (PF, EnKF, EKF) provide some information on the methodological spread, which however represents only one (difficult to characterize) part of the whole uncertainty. Further uncertainties are related to model biases, limited ensemble size, errors in the forcings and proxy data. Validation of the approaches using pseudo proxies in toy models and climate models and validation of the results using independent proxies is therefore particularly important. Any approach, however, fundamentally relies on a good understanding of the proxies.
affiliations
1Institute of Geography and Oeschger Centre for Climate Change Research, University of Bern, Switzerland; stefan.broennimann@giub.unibe.ch
2Department of Atmospheric Sciences, University of Washington, Seattle, USA
3Earth and Life Institute and Georges Lemaître Centre for Earth and Climate Research, Université catholique de Louvain, Belgium
4School of Geography, Earth and Environmental Sciences, University of Birmingham, UK
5Department of Physical Oceanography, Woods Hole Oceanographic Institution, USA
6Research Institute for Global Change, JAMSTEC, Yokohama Institute for Earth Sciences, Japan
7KNMI, De Bilt, The Netherlands
selected references
Full reference list online under: pastglobalchanges.org/products/newsletters/ref2013_2.pdf
Bhend J et al. (2012) Climate of the Past 8: 963-976
Dirren S, Hakim GJ (2005) Geophysical Research Letters 32, doi:10.1029/2004GL021444
Goosse H (2010) Journal of Geophysical Research 115, doi:10.1029/2009JD012737
van der Schrier G, Barkmeijer J (2005) Climate Dynymics 24: 355-371